Extracting Graph Topology from Image

The Problem

Now we have an image representing a graph, as shown in the figure below:

Suppose we already know the category of each pixel: background, node, or edge. How can we extract the graph topology from it and represent the graph by an adjacency matrix?

Challenges in Classical Algorithm

TODO

What about Neural Network?

We can use a simple algorithm to extract the position of each node. Suppose the position of a node is $\mathbf{P}(x,y)$, and there are $N$ nodes in total.

Then, the task is to fill in the $N\times N$ adjacency matrix with $0$ or $1$. As we can see, this can be converted into a binary classification problem.

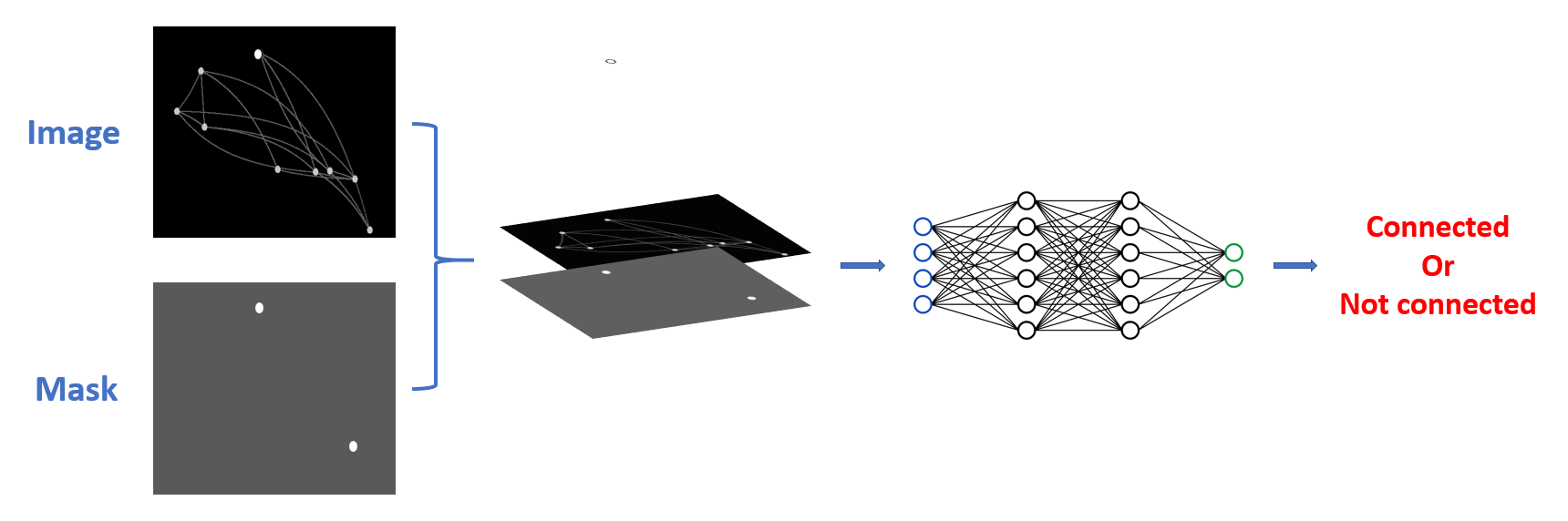
we can train a neural network $\mathbf{f}$, which takes 3 input: the image $I$, the position of a node pair $\left( \mathbf{P}_ 1, \mathbf{P}_ 2
\right)$. It outputs $O\in{0,1}$, indicating whether there is a direct connection between the node pair, i.e.,

$$O=\mathbf{f}(\mathbf{I}, \mathbf{P}_ 1, \mathbf{P}_ 2).$$

The dataset can be synthesized by a simple program, and we can use any classification network (e.g., EfficientNet) as our network architecture.

The problem is how to feed $\left( \mathbf{P}_ 1, \mathbf{P}_ 2
\right)$​ into the network. We can add an additional “mask channel” to the image, where the pixels belonging to the two input nodes are marked as 1, and the others as 0. Finally, we input this 4-channel “image” into the network.

Other Notes

TODO