Latency in LLM Serving
Preface
There have been many excellent works on LLM serving, mainly focusing on improving the throughput. Meanwhile, in practical applications, latency is equally important for LLM serving. However, currently few works focus on improvement of LLM serving latency, especially the latency optimization under SLA constraint.
This blog attempts to summarize the basic concepts and problems in this direction, and give some novel research directions based on some analysis of latency in LLM serving.
Latency Metrics
In LLM serving, we mainly focus on three latency metrics:
- TBT ($t_ {tbt}$): Time Between Tokens.
- TTFT ($t_ {ttft}$): Time to First Token.
- TE2E ($t_ {e2e}$): Time of End-to-end.
In practice, rather than the average or median latency, we usually consider the latency SLA, which means that 50%, 90%, and 99% of data should fall below certain thresholds.
Where The Latency Comes From?
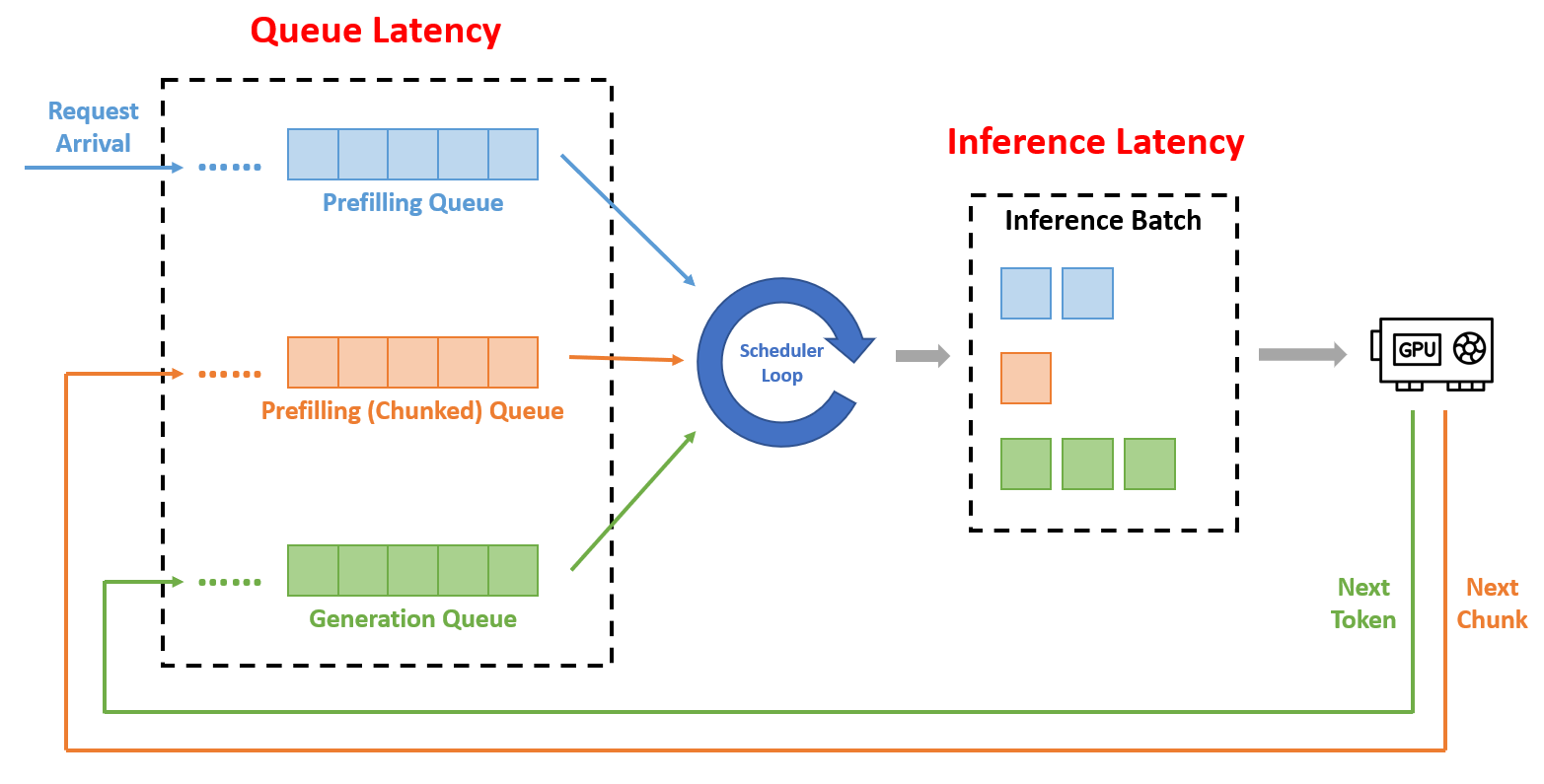
As shown in the figure above, the current popular LLM serving systems (such as vLLM, DeepSpeed) adopt an iteration-level scheduling strategy. The processing of each request is divided into the prefilling stage (prompt inference) and the generation stage (auto-regressive token-by-token generation). For systems such as Sarathi-Serve, the prompt is chunked to improve throughput, thus adding a chunked prefilling stage.
The LLM serving system maintains 3 queues to store requests in these 3 states. The scheduler runs in a loop, and in each iteration, it selects requests from these 3 queues with a certain strategy, and combines them into a batch for the inference engine.
In such systems, the latency of requests mainly comes from 2 aspects: queue latency and inference latency. Assuming the latencies for a request from being added into the prefilling queue, chunked prefilling queue, generation queue to being selected by scheduler are $t_ {qp}$, $t_ {qc}$, $t_ {qg}$ respectively, and inference latency of engine if $t_ {inf}$.
We get:
$$\begin{aligned}
t_ {ttft} &= t_ {qp} + (N_ {chunk} - 1) \cdot t_ {qc} + N_ {chunk} \cdot t_ {inf}, \\
t_ {tbt} &= t_ {qg} + t_ {inf}, \\
t_ {e2e} &= t_ {ttft} + N_{token} \cdot t_ {tbt},
\end{aligned}$$
where $N_ {chunk}$ is the chunk number of a prefilling request, $N_ {chunk}=1$ means no chunking. $N_ {token}$ is the total token number generated by a request.
Obviously, $t_ {inf}$ is not a fixed value. It’s related with the ingredient of the batch. We can denote it as:
$$t_ {inf} = f\left( B_ {p}, B_ {c}, B_ {g}, \mathbf{L}_ {p}, L_ {chunk} \right),$$
where $B_p$, $B_c$, $B_g$ indicates the number of non-chunked prefilling request, chunked prefilling request, generation request respectively. Vector $\mathbf{L}_ {p}$ means the prompt length of each non-chunked prefilling request in the batch.
$L_ {chunk}$ is the chunk size.
How to Improve It?
Based on the above analysis, we can find that reducing latency mainly involves reducing both queue latency and inference latency. In fact, some techniques, such as iteration-level scheduling and chunked prefilling, can be seen as improvements to queue latency.
On the other hand, improvement of inference latency have not received much attention. One reason is that, for inference engines, there is a trade-off between latency and throughput.
Generally speaking, higher batch size means higher throughput, but also higher inference latency. Techniques such as quantization and Paged Attention focus on more efficient memory usage to increase batch size, but inference latency may also increase accordingly (TODO: add an example), which means $t_ {tbt}$ and $t_ {ttft}$ may be increased, and SLA requirements are broken.
Therefore, there is an opportunity to improve inference latency in current LLM serving systems. The target may be an SLA-aware scheduler, which can maximize throughput without breaking SLA requirements. It should be able to dynamically decide the batch size and batch composition instead of just deploying a static prefilling-prioritize or generation-prioritize strategy.
I believe the key to this design is to predict $t_ {inf}$ to provide latency optimization guidance for the scheduler. Prediction based on profiling results may be a simple approach, but a performance model based on GPU computation capability and memory bandwidth might be more general.
Once we can predict $t_ {inf}$, $t_ {qp}$, $t_ {qc}$, and $t_ {qg}$ can also be predicted using mathematical tools such as Queueing Theory (e.g., Poisson distribution), allowing us to optimize serving for the following scenarios:
- When the request arrival rate is less than the maximum throughput: we can appropriately reduce batch size to improve $t_ {tbt}$.
- When the request arrival rate is greater than the maximum throughput: we can adjust the batch composition dynamically based on queue length, or drop some requests to avoid starvation.
- When the request arrival rate suddenly increases: we can adjust the batch composition to avoid breaking the SLA of $t_ {ttft}$.
In summary, this SLA-aware scheduler should provide better results than a static scheduler by considering arrival rate, queue length, and predicted $t_ {inf}$.
Some Meaningful Experiment Result
TODO